P=NP problem
Autor: Luka Hadži-Đokić
Od svog začetka, teorijsko računarstvo bavilo se rešavanjem problema uz pomoć opipljivih ili zamišljenih mašina koje pokreću i izvršavaju algoritme. Ono što su primetili matematičari i računarski naučnici koji su se ovim bavili jeste da postoje problemi koji su nerešivi, dok su kasnije našli da se oni rešivi lako mogu razvrstati po vremenu (ili memoriji) koje je potrebno da bi se algoritam izvršio. Tako je nastala teorija izračunljivosti, a kasnije i ovaj naizgled lak (a posle temeljne inspekcije đavolski težak) problem: „Koji je odnos klasa P i NP?”, poznatiji kao „P=NP” problem. Njega su formalno definisali (nezavisno jedan od drugog) Stiven Kuk (eng. Stephen Cook) i Leonid Levin, 1971. godine. Uvidevši moguće posledice koje bi izazvalo rešenje, 2000. godine je zajedno sa još šest drugih otvorenih pitanja svrstan među „Milenijumske probleme”, pa je tako nagrada za njegovo savladavanje u iznosu od milion dolara ponuđena od strane Klejovog matematičkog instituta (eng. Clay Mathematics Institute). Kao uvod u problem, moramo prvo definisati šta tačno znače P i NP.
Klasa P predstavlja one probleme koji se za ulazni podatak veličine n mogu rešiti u c·nk koraka (polinomijalno vreme rešavanja), gde su c i k nepromenljivi (ne zavise od veličine ulaznog podatka). Klasa NP predstavlja probleme čije je rešenje moguće proveriti polinomijalnim algoritmom. Ovo se u neformalnom govoru može objasniti na sledeći način: u klasu P spadaju problemi koji se lako rešavaju, a u klasu NP spadaju oni koji se lako proveravaju. Iz ove definicije izvodimo da svi problemi iz P spadaju i u NP klasu, jer ono što je lako rešiti, lako je i proveriti.
Ostatak NP čine problemi do čijeg se rešenja dolazi teško, u c·kn koraka (eksponencijalno vreme izvršavanja), ali se ipak ono lako potvrđuje. Primer za ovo bi bio problem nalik sledećem: „U nekom studentskom domu treba izabrati 100 studenata od ukupno 400 koji mogu biti primljeni u dom. Uz zadatak, dobili smo i listu parova učenika koji, iz nama nepoznatih razloga, ne smeju biti zajedno na spisku.” Da bismo napravili raspored, jedino što možemo uraditi jeste da probamo sve moguće kombinacije „student-soba” i da potom svaku uporedimo sa listom koju smo dobili. Od 400 studenata izabrati odgovarajućih 100 je praktično nemoguće, jer broj mogućih kombinacija nadmašuje ukupan broj atoma u nama poznatom univerzumu (za neke manje brojeve je moguće rešiti, ali broj koraka naglo raste sa povećanjem ulaznog podatka). U odnosu na to, da bismo proverili jedno rešenje ovog problema, sve što treba da uradimo jeste da izabranih 100 uporedimo sa listom.
Još jedan bitan slučaj klase NP su NP-kompletni problemi – specifični su po tome što se svaki drugi problem iz klase NP na njih može svesti. Tu spadaju problemi trgovačkog putnika, problem zadovoljivosti (SAT problem, koji je u stvari prvi dokazan kao član NP-kompletnih problema, Kuk-Levinovom teoremom) i mnogi drugi. Trgovački putnik je, na primer, problem koji postavlja pitanje da li je, uz pomoć karte sa nekim gradovima i dužine puta između svakog grada, moguće proći kroz svaki od tih gradova i vratiti se u početni, tako da dužina celog puta bude manja od proizvoljno izabrane dužine L. Kada bi neko za ovaj ili neki od ostalih takvih problema našao „lako” rešenje (ono koje se izvršava u polinomijalnom vremenu) i tako ga svrstao u grupu P, dokazao bi da se, u stvari, cela grupa NP može svesti na jedan P problem, što bi dovelo do njihove jednakosti (P=NP). Ovakvo rešenje tog gigantskog pitanja računarstva imalo bi, bez preterivanja, u isto vreme užasavajući i ohrabrujući efekat. Naime, ako bi ono bilo istinito, šifrovanje podataka bi izgubilo svoj smisao (jer se oni šifruju pod pretpostavkom da je jedan problem koji spada u NP skoro nemoguće rešiti), ali bi isto tako i omogućilo lako rešavanje mnogih drugih problema. Kako je to rekao dr Skot Aronson (eng. Scott Aaronson) sa MIT-a: „Ako je P=NP, onda bi svet bio dosta drugačije mesto nego što mi pretpostavljamo da jeste. ‘Kreativni skokovi’ ne bi imali nikakvu specijalnu vrednost, osnovna praznina između rešavanja problema i prepoznavanja njegovog već pronađenog rešenja takođe bi nestala. Svako ko shvata vrednost simfonije postao bi Mocart; svako ko može da proprati korake argumenta bio bi Gaus.”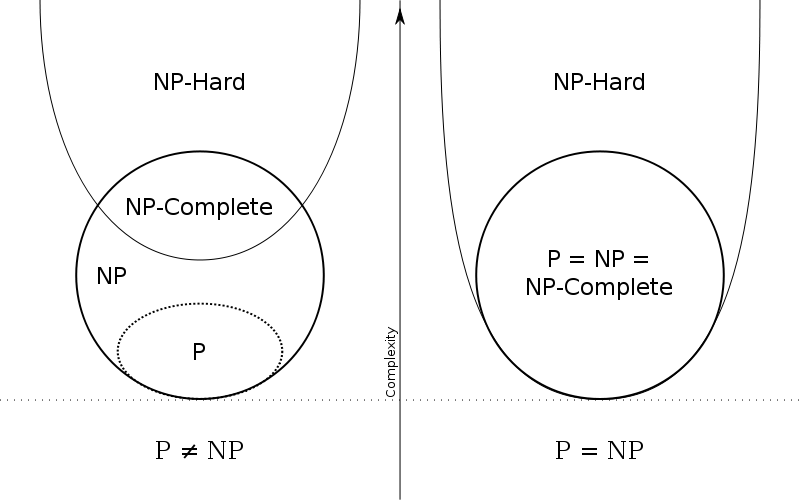
Međutim, ako je verovati stručnjacima, čije je znanje i shvatanje ovog problema na mnogo višem nivou od nas koji o njemu pročitamo u časopisu ili drugde na internetu, tako nešto je vrlo malo verovatno. U anketi sprovedenoj 2002. godine, od 100 računarskih naučnika 61 je mišljenja da je odgovor P≠NP, njih 22 nije bilo sigurno, 8 je verovalo da je dolaženje do rešenja nemoguće, dok je samo 9 njih reklo da je odgovor P=NP.
Uprkos tome, i uprkos činjenici da već više od četrdeset godina dokaz ne postoji (iako se radi o jednom od najpoznatijih problema u matematici ili računarstvu), mnogi budući ili trenutni umovi naše planete izlazili su u javnost sa „rešenjem” i zbog toga su bili ili ismevani ili prosto ignorisani od strane stručnog kadra. Dok se slažemo da je za rešenje potrebna disciplina i usavršen matematički um (koji se stiče godinama rada u ovom polju), nadamo se da će saznanje o ovom problemu (uz našu pomoć ili pomoć svemogućeg interneta) inspirisati dovoljno genijalnih ljudi da se, počevši od formalnog obrazovanja (praćenog mukotrpnim istraživanjem ove grane računarske nauke), sudare sa P i NP i zaista pobede, a sa današnjim akademicima duboko saosećamo, jer će biti primorani da čitaju sve one očigledno netačne dokaze matematičara u pokušaju dok se ne nađe onaj pravi.
