Numerička obrada i simulacije (3. deo)
Autor: Stefan Nožinić
Upoznali smo se sa nekim osnovnim principima i problemima na koje možemo naići tokom numeričke obrade podataka, te je red da malo detaljnije istražimo kakvi su nam alati na raspolaganju. Pomenuli smo da postoje i komercijalni i slobodni alati za ovu namenu, od kojih se neki češće koriste a neki ređe. Uglavnom, situacija je takva da svi ti alati mogu da rade 99% stvari koje su nam neophodne (prim. aut.). Naravno, neke stvari se lakše postignu drugim alatom nego nekim koji mi koristimo. Svaki alat je specifičan. U ovom serijalu ćemo se fokusirati na jedan skup alata kako bismo, pored teorije, pokazali i kako se problemi rešavaju u praksi. Zbog ovoga, ovaj tekst posvećujemo detaljnom opisu onog šta ćemo koristiti. Neke od ovih alata ste verovatno upoznali čitajući naš časopis, ali ćemo ih ovde ponovo pomenuti radi preglednosti i kompletnosti. Osnova svega će nam biti programski jezik Pajton. On je vrlo jednostavan po sintaksi i ono što nam se dopada kod njega jeste činjenica da vas jezik tera da pišete lep kôd (prim. aut.). Možda vam ovo trenutno ne znači ništa, ali može biti krucijalno prilikom uklanjanja grešaka u vašim programima (simulacijama i sličnom). Pored toga, jezik ima sjajan skup standardnih biblioteka za razne stvari i dobru dokumentaciju. Ima veliku zajednicu pa nećete biti uskraćeni za određenu informaciju o samom jeziku i najboljoj praksi. Mnogo naših autora koristi ovaj jezik za svoje projekte, pa se nemojte ustručavati ni da kontaktirate sa nama putem naše adrese elektronske pošte, ili da nas posetite na IRC-u ili na našim stranicama na Fejsbuku i Tviteru. Pored toga što Pajton ima lepu kolekciju raznih biblioteka, nedostaju mu neke stvari koje ćemo morati da uzmemo sa strane. To su biblioteke za crtanje grafika i vizuelizaciju podataka (eng. plotting) i biblioteka za rad sa matricama. Sve ovo se nalazi u paketu Sajpaj (eng. SciPy) koji uključuje i neke dodatne stvari. Ovo je poprilično popularna biblioteka, pa se tako nalazi u većini zvaničnih riznica paketa na svim poznatijim distribucijama linuksa kao i na BSD distribucijama. Postoje verzije za vindouz i Mek OS X. Ako niste upoznati sa Pajtonom, preporučujemo vam da pregledate dokumentaciju za početnike. Naša procena je da se Pajton može naučiti jako brzo. Ako imate nekih problema, znate gde da nas tražite. Kada instalirate ovu biblioteku, njene komponente kao što su Numpaj (eng. NumPy) i Matplotlib (eng. Matplotlib) možete da koristite tako što ih uključite u program:
import numpy as np
import matplotlib.pyplot as plt
Potom možete da nacrtate svoj prvi grafik:
x = np.linspace(0, 100, 1000)
plt.plot(x, np.sin(x))
plt.show()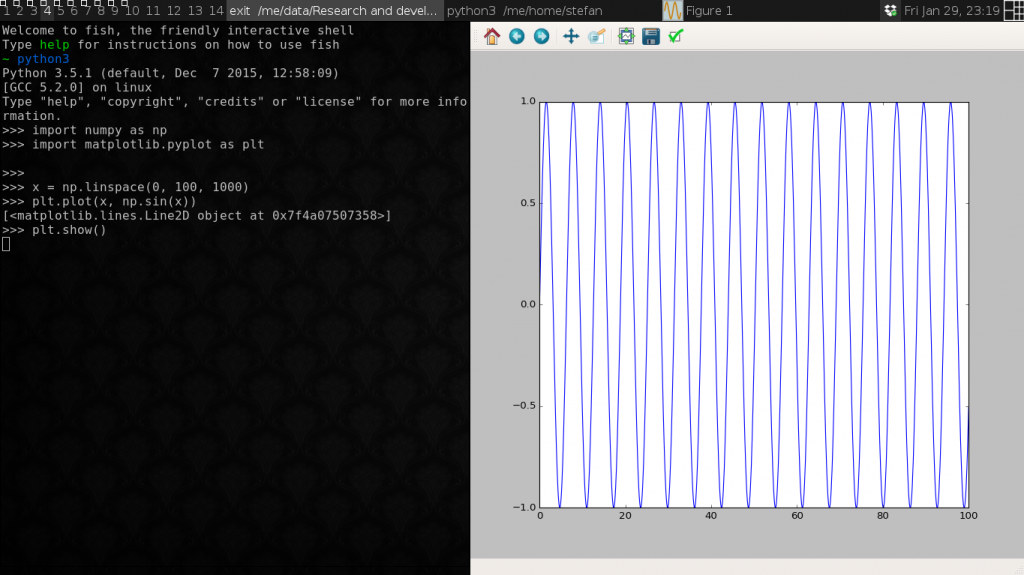
U ovom kodu se prvo generiše niz od 1000 brojeva koji predstavlja raspon od 0 do 100. Ovo zamislite kao brojevnu pravu gde je deo od 0 do 100 podeljen na hiljadu delova. Posle se poziva plot funkcija koja uzima dva glavna argumenta:
x-osa, brojevi koji će biti prikazani na x-osi
y-osa, brojevi koji odgovaraju datoj vrednosti iz prvog niza na toj poziciji.
Naravno, jasno je da ova dva niza moraju imati istu veličinu. Kako mi generišemo te nizove? Prvi smo generisali pomoću funkcije linspace koju smo gore objasnili. Ona nam je vratila niz od 1000 brojeva. Drugi niz smo generisali pomoću funkcije np.sin kojoj smo kao parametar prosledili prvi niz x, a ona nam vraća niz iste veličine, takav da je na i-toj poziciji vrednost sinusa od broja koji se nalazi na i-toj poziciji u prosleđenom nizu, odnosno u nizu x. Ovde je bitno shvatiti da su sve funkcije u Numpaju vektorizovane. To znači da kao argument ne primaju jedan broj, već niz brojeva (vektor) i vraćaju novi niz brojeva (vektor). Da budemo još generalniji, funkcije mogu primiti tenzor (višedimenzionalan niz) i vratiti nam tenzor. To zapravo znači da sve operacije moramo raditi koristeći funkcije koje su vektorizovane i moramo izbeći korišćenje for petlji jer na ovakav način dobijamo na brzini. Dobra strana ovakvog razmišljanja jeste što se kasnije kôd lako može prebaciti na grafičku karticu koja, na primer, mnogo brže vrši množenje matrica od standardnog procesora. Zbog ovakvih kriterijuma je važno koncept osmisliti prvo na papiru, pa ga potom isprogramirati, a za to je potrebno dosta teorijskog znanja iz matematike koja leži ispod svake obrade podataka i numeričke simulacije. Zbog toga ćemo posvetiti sledeći deo serijala upravo tome — pokušaćemo da obradimo potrebnu teoriju kako bismo kasnije lakše mogli da iskoristimo pun potencijal alata koji su nam dati.