Numerička obrada podataka i simulacije (6. deo)

Autor: Stefan Nožinić

Često nakon obrade nekih podataka, naprimer nakon neke simulacije, želimo da rezultate vizuelno prikažemo kako bi nam bilo lakše da ih bolje razumemo. Očigledno je da će nam za ovo trebati grafičko okruženje. Ako ste nekada programirali grafičke aplikacije, sigurno znate koliko je vremena potrebno za programiranje aplikacije koja iscrtava grafikon sa svim mogućnostima zumiranja, skaliranja i pomeranja. Kako je vizuelizacija podataka sve bitnija u odlučivanju da li neki rezultati imaju smisla ili ne, pojavila se potreba za programskim bibliotekama za brzo iscrtavanje grafika raznih tipova.

Matplotlib (eng. Matplotlib) je baš takva biblioteka. Pisana je u Pajtonu i vrlo se lako koristi. Pored toga što je dosta intuitivna za korišćenje, dokumentacija iste je jako bogata primerima koda i slikama.

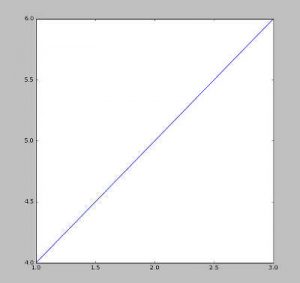
Najjednostavniji način da napravite grafikon koji spaja date tačke je sledeći:

>>> import matplotlib.pyplot as plt >>> plt.plot([1,2,3], [4,5,6]) [] >>> plt.show()

Primetite da kao prvi argument plot funkcije prosleđujemo x vrednosti a kao drugi y vrednosti.

Naravno, kako svaka funkcija u NumPaj biblioteci vraća niz za dati niz, odnosno vektorizovana je – možemo lako crtati i grafikone funkcija bez ikakvog for ciklusa eksplicitno.

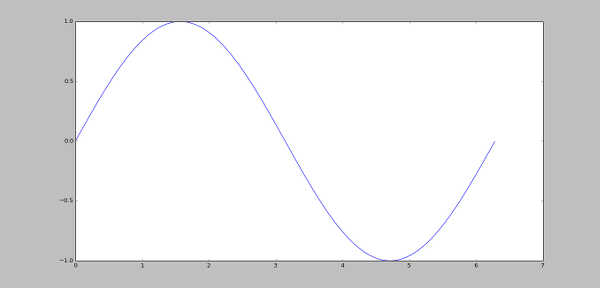
Primer dajemo za crtanje grafika sinusne funkcije:

>>> x = np.linspace(0, 6.28, 10000) >>> y = np.sin(x) >>> plt.plot(x,y) [] >>> plt.show()

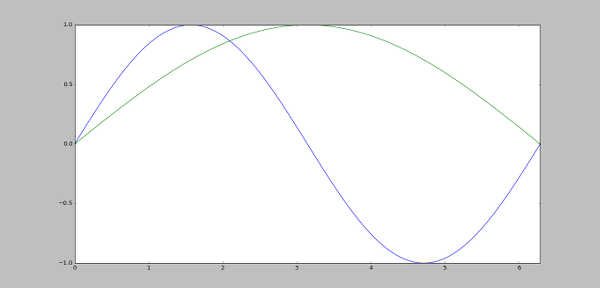
Na jednoj slici možemo nacrtati i više grafikona. Za svaki poziv plot funkcije pre show Matplotlib će generisati dodatnu krivu i njoj dodeliti boju tako da se lakše razlikuje od prethodne.

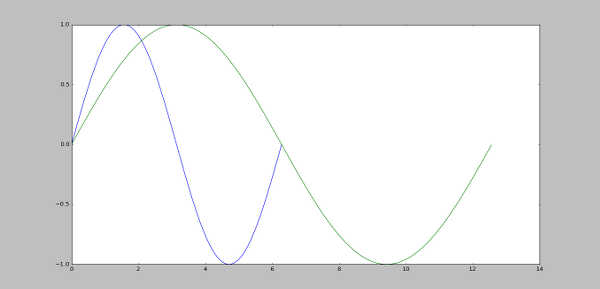
>>> plt.plot(x,y) [] >>> plt.plot(2*x,y) [] >>> plt.show()

Primetite da je plava kriva prekinuta na polovini. Ovo se dešava jer nema podataka za naredne vrednosti. Ako želimo da ograničimo naš grafikon na određeni opseg, koristimo xlim i ylim funkcije.

>>> plt.plot(x,y) [] >>> plt.plot(2*x,y) [] >>> plt.xlim(0, 6.28) (0, 6.28) >>> plt.show()

Grafikon je moguće zumirati, pomerati i moguće ga je sačuvati kao png sliku koju kasnije možete zasebno publikovati negde.

Moguće je učitati i neku postojeću sliku, na njoj izvršiti neke transformacije i to onda plotovati:

>>> img = plt.imread("libre.png") >>> plt.imshow(img)  >>> plt.show()

Potrebno je primetiti da je ovde img matrica koja predstavlja našu sliku.

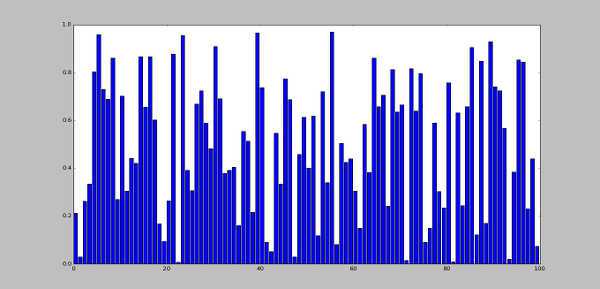
Histogrami se isto lako iscrtavaju pomoću bar funkcije.

>>> x = np.arange(100) >>> y = np.random.random(100) >>> plt.bar(x,y)  >>> plt.show()

Naravno, sam izgled bar plota se može dodatno podešavati kroz pozive drugih funkcija koje detaljnije možete izučiti u dokumentaciji.

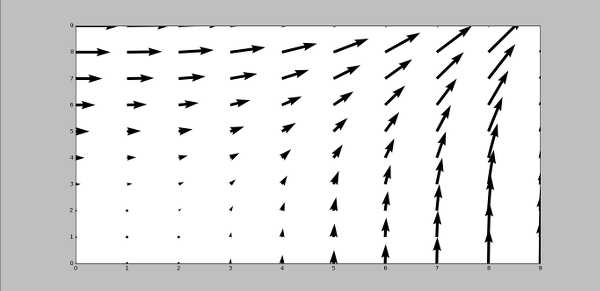
Vektorska polja su grafikonske funkcije koja u određenoj poziciji predstavlja vektor. Primer ovakvih funkcija je brzina vetra. Brzina ima smer, intenzitet i pravac. U svakoj tački je (obično) različita.

>>> y,x = np.mgrid[0:10:1, 0:10:1] >>> u = y**2 + 1 >>> v = x**2 >>> plt.quiver(u,v)  >>> plt.show()

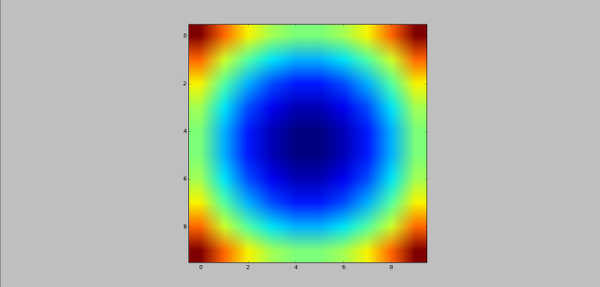
Zanimljiva je primena mgrid matrice (primetite da su x,y matrice i to x se ne menja po koloni a y po redu). Ovo je jako korisno za brzu evaluaciju funkcija u datim tačkama.

>>> f = (x-4.5)**2 + (y-4.5)**2 >>> plt.imshow(f)  >>> plt.show()

U sledećem delu ćemo sve ovo primeniti kako bismo uspeli da simuliramo neke fizičke procese rešavanjem diferencijalnih jednačina.