GeoGebra
Autor: Stefan Nožinić
Ako ste pravi geek onda zasigurno ne može da prođe dobar osećaj kada rešite jedan matematički problem. Matematika je jako zanimljiva nauka ali nije redak slučaj da ponekad nemamo vremena da rešavamo nešto banalno. Poenta je usredsrediti se na nešto kompleksnije a onaj banalni deo koji često zamara i tera ljude da odustanu od problema, rešava naš računar. Ovaj program, koji predstavljamo ima baš tu namenu. U pitanju je slobodan program za geometrijska crtanja, proučavanje grafika funkcija i još mnogo toga. Geogebra se može instalirati i pokrenuti na linuksu i nekim vrstama UNIX-a, na MS Windowsu i na Mac OSX operativnom sistemu. Takođe, možemo je koristiti i online ako želimo. Pisana je u Java programskom jeziku tako da je moguće portovati na sve platforme koji podržavaju java runtime.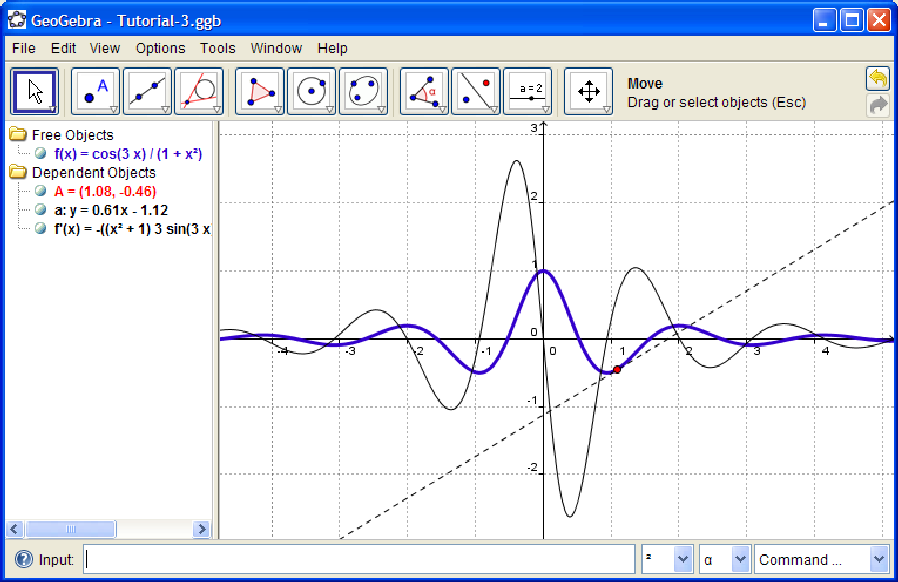
Mogućnosti
GeoGebra može da obrađuje geometrijske funkcije kao što su crtanje tačaka, linija, trouglova, krugova, uglova i još mnogo toga. Takođe može i da nacrta grafik neke funkcije što dosta može pomoći u matematičkoj analizi. Možemo da vidimo, na primer, u kojoj tački dve funkcije imaju istu vrednost, možemo da konstruišemo svašta i još mnogo drugih stvari.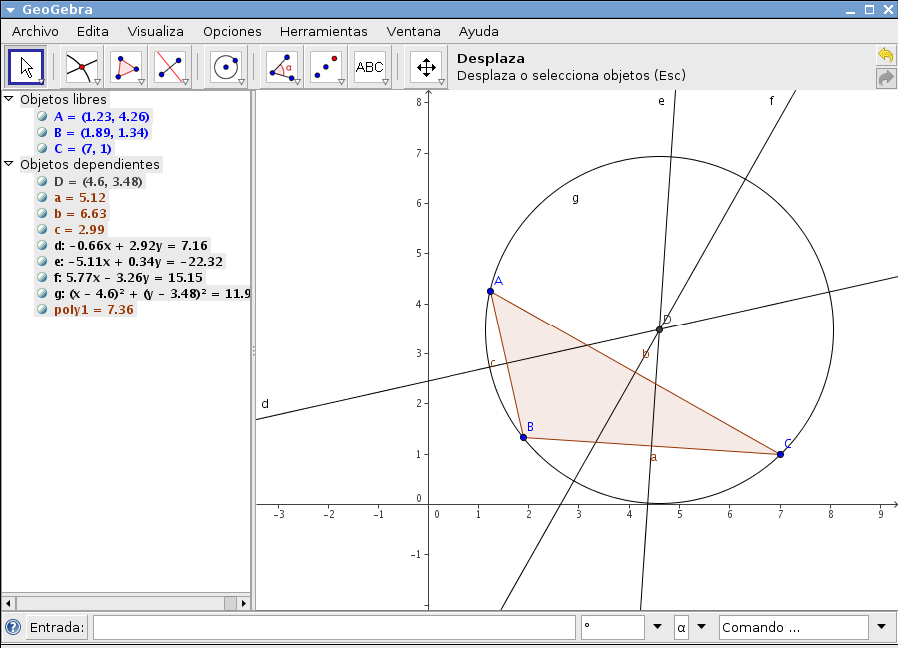
Mi navodimo jedan primer korišćenja GeoGebra-e.
Konstrukcija jednakostraničnog trougla:
Korak 1: Prvo kada pokrenemo GeoGebra-u vidimo Dekartov koordinatni sistem. Pošto nam on za ovo nije potreban možemo ga isključiti putem opcije View→Axes.
Korak 2: Izaberemo alatku „Segment between two points“ i izaberemo neke 2 tačke. Dobijamo duž AB
Korak 3: Izaberemo alatku „Circle with center through point“ i kliknemo na tačku A pa onda na tačku B. Dobijamo sledeće: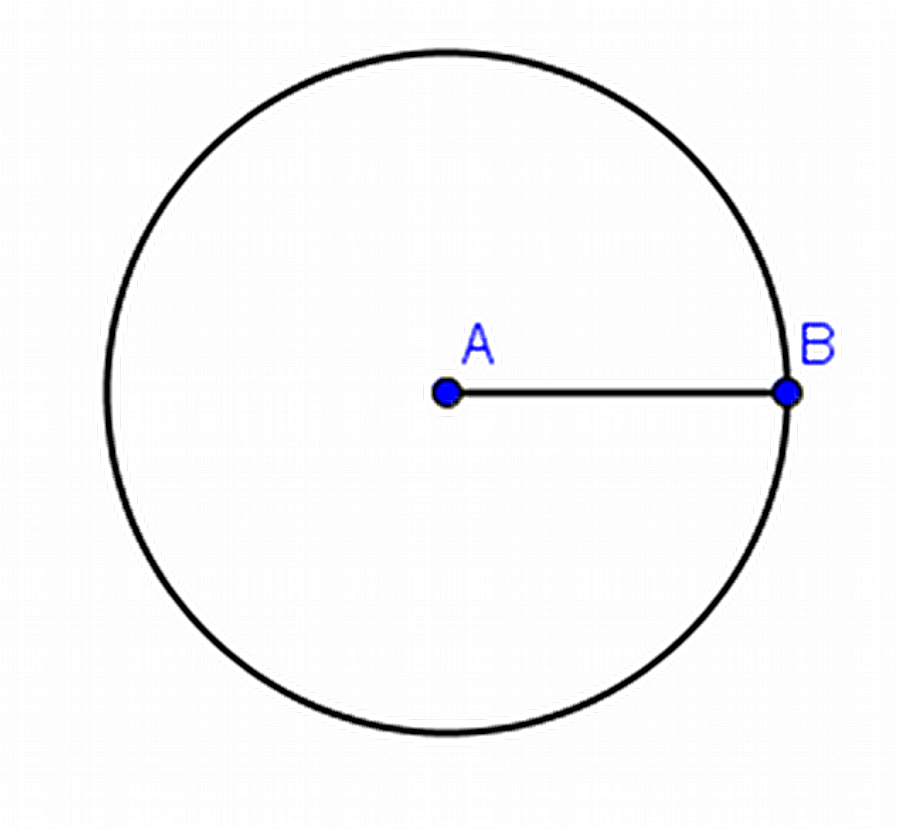
Korak 4: Sada sa istom alatkom kliknemo na tačku B pa onda na tačku A. Sada imamo 2 kružnice koje se seku u 2 tačke.
Korak 5: da obeležimo te 2 tačke koristimo alatku „Intersect two objects“. Kliknemo na jednu pa onda na drugu kružnicu. Dobijamo tačke C i D koje su tačke preseka.
Korak 6: Sada ćemo konstruisati trougao koji nam treba. Kliknemo na „Polygon“ i potom kliknemo na tačke ABCA redom. Dobili smo trougao.
Korak 7: kliknemo na opciju „Angle“ i potom kliknemo na tačke redom: CABABCBCA i time smo dobili prikaz sva 3 unutrašnja ugla ovog trougla. Primećujemo da su sva 3 jednaka i to po 60 stepeni. Sada Kliknemo na alatku „Move“ i pokušamo pomerati tačke, primećujemo da se uglovi ne menjaju.
Eto to je bio jedan primer korišćenja ovog fantastičnog programa koji preporučujemo.