Numerička obrada i simulacije (7. deo)
Autor: Stefan Nožinić
Kako se opisuju fizički sistemi
Svaki fizički sistem ima neki model koji ga opisuje ili aproksimira. Najjednostavniji primer je padanje loptice na pod. Mi znamo da na lopticu deluje gravitaciona sila i na osnovu toga primenjujemo drugi Njutnov zakon. Za datu lopticu imamo jednačinu koja nam opisuje koliko u datom trenutku iznosi ubrzanje loptice. Kako naša loptica ima isto ubrzanje u svakom trenutku – gravitaciona sila se ne menja, što znači da se njena brzina menja linearno (povećava se) a da se pređeni put može opisati kvadratnom funkcijom. Kako ovo znamo? Ubrzanje je promena brzine u jedinici vremena (izvod brzine), a brzina je promena pređenog puta u jedinici vremena, odnosno ubrzanje je drugi izvod pređenog puta. Kako naš model iskazuje koliko je ubrzanje loptice, mi moramo da to ubrzanje integralimo dva puta kako bismo dobili pređeni put. Jednačina koja opisuje kretanje loptice je diferencijalna jednačina.
Zapravo, svaki fizički sistem se može opisati kao diferencijalna jednačina.
Diferencijalne jednačine prvog reda
Ovaj tip je osnovni tip diferencijalne jednačine. Za datu funkciju x (koja može biti pozicija ili nešto drugo) diferencijalna jednačina je:
Sa leve strane nam se nalazi promena funkcije u zavisnosti od promene vremena, a sa desne strane nam se nalazi vrednost te promene.
Ojlerov metod za rešavanje diferencijalne jednačine prvog reda
Najjednostavniji način da rešimo gore opisani tip jednačine je sledeći:
Ako imamo vrednost naše funkcije u nekom trenutku i ona iznosi , mi želimo da odredimo narednu vrednost funkcije. Kako su računari diskretne mašine i ne možemo previše ići u detalje – ne možemo odrediti vrednost funkcije baš u svakom trenutku. Ono šta možemo uraditi jeste da izračunamo u približnom trenutku posle
vremena odnosno da odredimo
.
Ovo možemo uraditi baš zahvaljujući postavci naše jednačine jer je:
Kada ovo sredimo, imamo Ojlerov korak za naredni vremenski korak:
Diferencijalne jednačine drugog reda
Ovo su složenije jednačine, ali se vrlo lako prebacuju na jednačine prvog reda. One su oblika: odnosno, može se i lakše zapisati kao
Ako bi nam
bio pređeni put onda je
brzina, a
nam je ubrzanje.
Kako ovo rešavamo? Uvedemo smenu i onda imamo sledeću situaciju:
i
Prvo rešimo prvu jednačinu pomoću Ojlerovog metoda, a onda novu vrednost za brzinu ubacimo u drugu:
Primer – kosi hitac
Evo i primera kako bismo uradili simulaciju bacanja loptice ukoso.import numpy as np
import matplotlib.pyplot as plt
# Prvo zadajemo pocetne vrednosti, imamo dve koordinate, radimo sa dve pozicije i dve brzine
# jedna za a druga za y koordinatu loptice
x = 0.0
y = 0.0
v_x = 10
v_y = 10
dt = 0.01 # vremenski pomeraj
def f_y(t, x, v):
return -9.81 # ubrzanje po y-osi na dole
def f_x(t, x, v):
return 0 # ubrzanje po x-osi
p_x = [x] # ovde čuvamo x vrednosti da plotujemo
p_y = [y] # ovde cuvamo y vrednosti da plotujemo
# uradimo nekoliko iteracija i dodajemo nove vrednosti u niz za plotovanje
for i in range(200):
t = i * dt
v_x = v_x + dt * f_x(t,x,v_x)
x = x + dt*v_x
v_y = v_y + dt * f_y(t,y,v_y)
y = y + dt * v_y
print(x)
print(y)
print()
p_x.append(x)
p_y.append(y)
plt.plot(p_x, p_y, "o")
plt.show()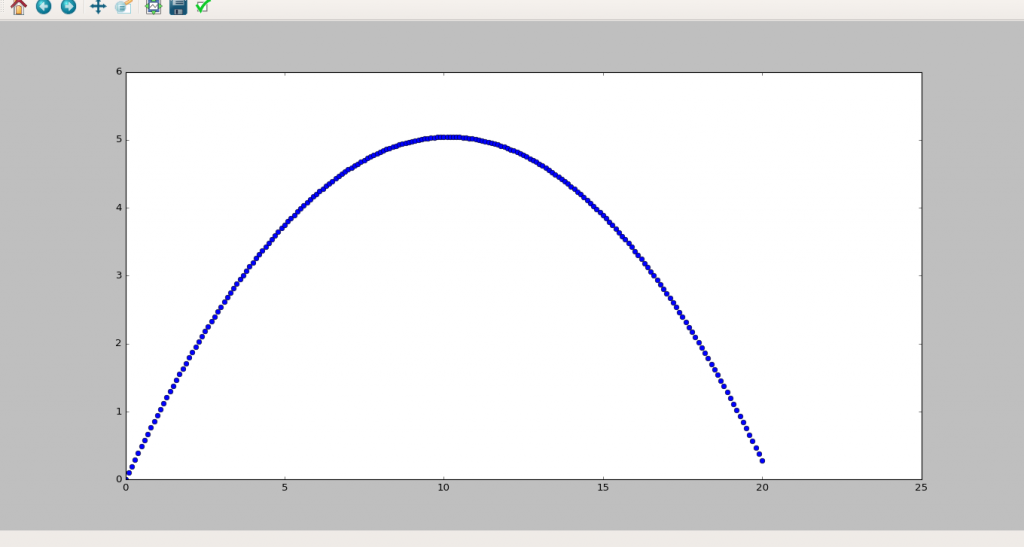 Potrebno je primetiti da ovde imamo dve pozicije, dve koordinate pošto radimo u dvodimenzionalnom sistemu. Kod možemo i kraće napisati ako definišemo poziciju i brzinu kao vektore.
Potrebno je primetiti da ovde imamo dve pozicije, dve koordinate pošto radimo u dvodimenzionalnom sistemu. Kod možemo i kraće napisati ako definišemo poziciju i brzinu kao vektore.import numpy as np
import matplotlib.pyplot as plt
# Prvo zadajemo pocetne vrednosti, imamo dve koordinate, radimo sa dve pozicije i dve brzine
# jedna za a druga za y koordinatu loptice
x = np.array([0,0])
v = np.array([10, 10])
dt = 0.01 # vremenski pomeraj
def f(t, x, v):
return np.array([0, -9.81]) # ubrzanje
p_x = [x[0]]
p_y = [x[1]]
# uradimo nekoliko iteracija i dodajemo nove vrednosti u niz za plotovanje
for i in range(200):
t = i * dt
v = v + dt * f(t,x,v)
x = x + dt * v
p_x.append(x[0])
p_y.append(x[1])
plt.plot(p_x, p_y, "o")
plt.show()
Dodatni metodi za numeričko rešavanje diferencijalnih jednačina
Često Ojlerov metod nije dovoljno stabilan ili tačan. Zbog ovoga postoje i druge metode kao što su Runga-Kuta i implicitni metodi. Predlažemo vam da pronađete na internetu kako se oni koriste kako ne biste dolazili do problema da vam Ojler ne rešava problem dovoljno stabilno ili tačno.