Нумеричка обрада и симулације (7. део)
Аутор: Стефан Ножинић
Како се описују физички системи
Сваки физички систем има неки модел који га описује или апроксимира. Најједноставнији пример је падање лоптице на под. Ми знамо да на лоптицу делује гравитациона сила и на основу тога примењујемо други Њутнов закон. За дату лоптицу имамо једначину која нам описује колико у датом тренутку износи убрзање лоптице. Како наша лоптица има исто убрзање у сваком тренутку – гравитациона сила се не мења, што значи да се њена брзина мења линеарно (повећава се) а да се пређени пут може описати квадратном функцијом. Како ово знамо? Убрзање је промена брзине у јединици времена (извод брзине), а брзина је промена пређеног пута у јединици времена, односно убрзање је други извод пређеног пута. Како наш модел исказује колико је убрзање лоптице, ми морамо да то убрзање интегралимо два пута како бисмо добили пређени пут. Једначина која описује кретање лоптице је диференцијална једначина.
Заправо, сваки физички систем се може описати као диференцијална једначина.
Диференцијалне једначине првог реда
Овај тип је основни тип диференцијалне једначине. За дату функцију x (која може бити позиција или нешто друго) диференцијална једначина је:
Са леве стране нам се налази промена функције у зависности од промене времена, а са десне стране нам се налази вредност те промене.
Ојлеров метод за решавање диференцијалне једначине првог реда
Најједноставнији начин да решимо горе описани тип једначине је следећи:
Ако имамо вредност наше функције у неком тренутку и она износи , ми желимо да одредимо наредну вредност функције. Како су рачунари дискретне машине и не можемо превише ићи у детаље – не можемо одредити вредност функције баш у сваком тренутку. Оно шта можемо урадити јесте да израчунамо у приближном тренутку после
времена односно да одредимо
.
Ово можемо урадити баш захваљујући поставци наше једначине јер је:
Када ово средимо, имамо Ојлеров корак за наредни временски корак:
Диференцијалне једначине другог реда
Ово су сложеније једначине, али се врло лако пребацују на једначине првог реда. Оне су облика: односно, може се и лакше записати као
Ако би нам
био пређени пут онда је
брзина, а
нам је убрзање.
Како ово решавамо? Уведемо смену и онда имамо следећу ситуацију:
и
Прво решимо прву једначину помоћу Ојлеровог метода, а онда нову вредност за брзину убацимо у другу:
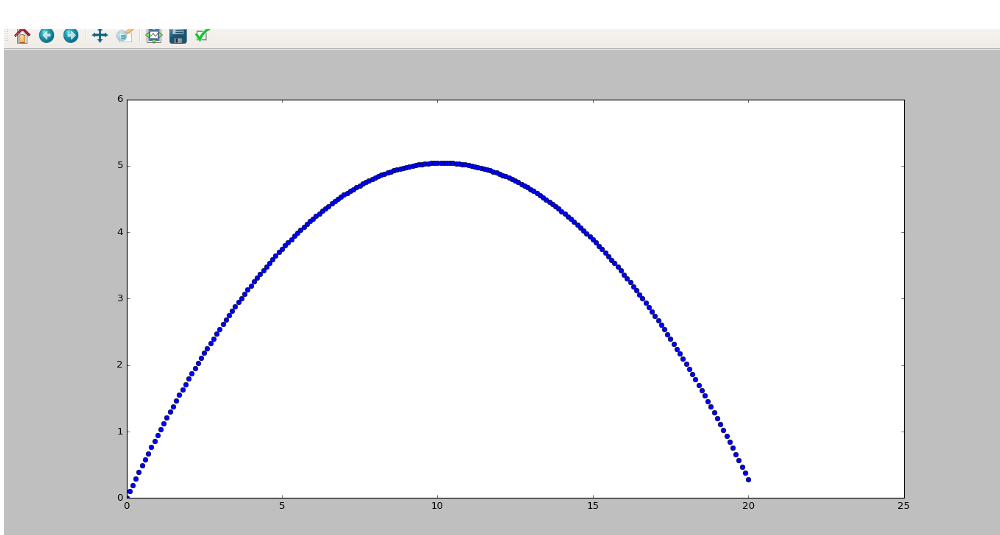
Пример – коси хитац
Ево и примера како бисмо урадили симулацију бацања лоптице укосо.
import numpy as np
import matplotlib.pyplot as plt
# Prvo zadajemo pocetne vrednosti, imamo dve koordinate, radimo sa dve pozicije i dve brzine
# jedna za a druga za y koordinatu loptice
x = 0.0
y = 0.0
v_x = 10
v_y = 10
dt = 0.01 # vremenski pomeraj
def f_y(t, x, v):
return -9.81 # ubrzanje po y-osi na dole
def f_x(t, x, v):
return 0 # ubrzanje po x-osi
p_x = [x] # ovde čuvamo x vrednosti da plotujemo
p_y = [y] # ovde cuvamo y vrednosti da plotujemo
# uradimo nekoliko iteracija i dodajemo nove vrednosti u niz za plotovanje
for i in range(200):
t = i * dt
v_x = v_x + dt * f_x(t,x,v_x)
x = x + dt*v_x
v_y = v_y + dt * f_y(t,y,v_y)
y = y + dt * v_y
print(x)
print(y)
print()
p_x.append(x)
p_y.append(y)
plt.plot(p_x, p_y, "o")
plt.show()
 Потребно је приметити да овде имамо две позиције, две координате пошто радимо у дводимензионалном систему. Код можемо и краће написати ако дефинишемо позицију и брзину као векторе.
Потребно је приметити да овде имамо две позиције, две координате пошто радимо у дводимензионалном систему. Код можемо и краће написати ако дефинишемо позицију и брзину као векторе.
import numpy as np
import matplotlib.pyplot as plt
# Prvo zadajemo pocetne vrednosti, imamo dve koordinate, radimo sa dve pozicije i dve brzine
# jedna za a druga za y koordinatu loptice
x = np.array([0,0])
v = np.array([10, 10])
dt = 0.01 # vremenski pomeraj
def f(t, x, v):
return np.array([0, -9.81]) # ubrzanje
p_x = [x[0]]
p_y = [x[1]]
# uradimo nekoliko iteracija i dodajemo nove vrednosti u niz za plotovanje
for i in range(200):
t = i * dt
v = v + dt * f(t,x,v)
x = x + dt * v
p_x.append(x[0])
p_y.append(x[1])
plt.plot(p_x, p_y, "o")
plt.show()
Додатни методи за нумеричко решавање диференцијалних једначина
Често Ојлеров метод није довољно стабилан или тачан. Због овога постоје и друге методе као што су Рунга-Кута и имплицитни методи. Предлажемо вам да пронађете на интернету како се они користе како не бисте долазили до проблема да вам Ојлер не решава проблем довољно стабилно или тачно.